B-tree & 인덱싱

23 Feb 2022

데이터베이스의 성능을 개선하는 방법중에 가장 먼저 떠오르는 것은 단연 인덱스를 생성하는 것이다. 오늘은 인덱스의 내부 작동 원리에 대해 알아보려고 한다. 물론 각 데이터베이스마다 세부적인 방식에 차이가 있겠지만, 대표적으로 많이 쓰이는 인덱싱 방법인 B-tree에 대해서 알아보자.

B-tree란?

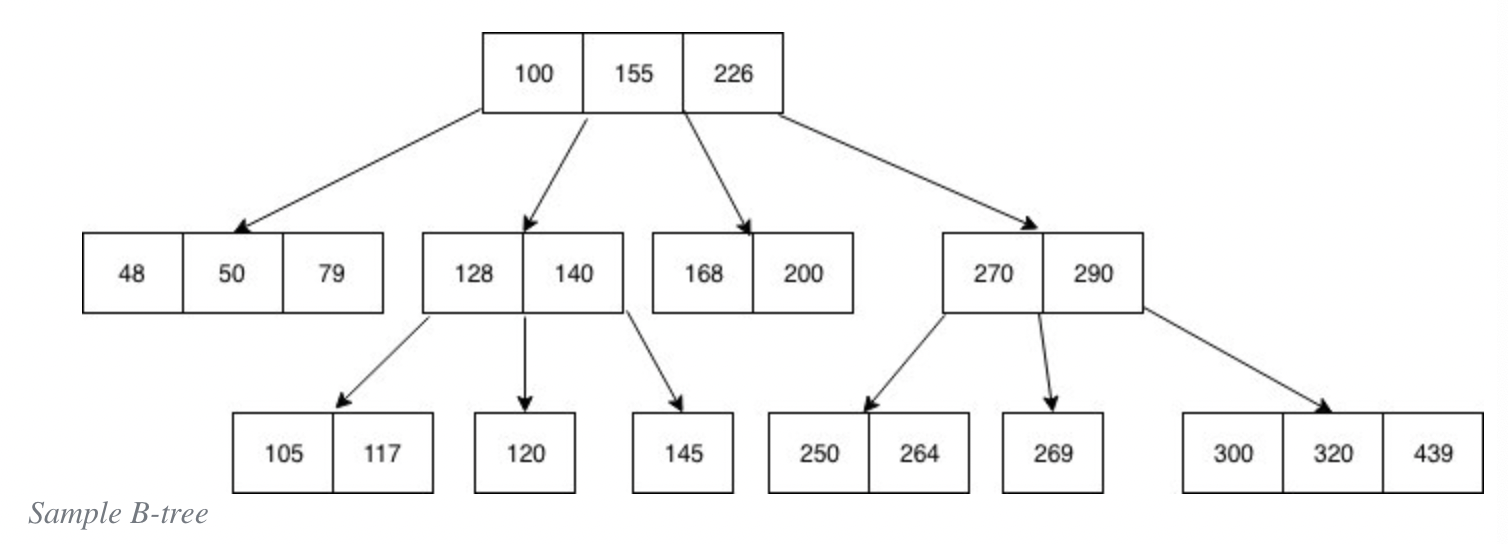
B-tree는 트리방식의 자료구조인데, 노드의 순서를 고려한 트리구조라고 보면 되겠다.

각 노드는 하나의 숫자키가 아닌 여러개의 숫자키를 담고 있는데, 특징을 보자면:

• 각 노드의 키는 오름차순으로 정렬되어 있다
• 각각의 키는 최대 포인터 두개를 가지고 있으며, 각 포인터는 하위 노드를 가리킨다
• 숫자키의 왼쪽 포인터가 가리키는 노드는 더 작은 숫자들로 이루어진 노드, 오른쪽 포인터가 가리키는 노드는 더 높은 숫자들로 이루어진 노드이다.
• 한 노드가 ‘n’개의 숫자키를 가지고 있다면, 포인터의 개수는 최대 ‘n+1’이 된다.

자, 그럼 이 b-tree가 데이터베이스에서 많이 사용되는 이유는 무엇일까?

데이터베이스는 말그대로 데이터를 저장하는 곳으로, 그 일을 잘 수행하기 위해서 b-tree라는 자료구조가 내부적으로 사용되어 진다.

b-tree를 잠시 잊고, array 즉 리스트라는 자료구조에 데이터를 저장한다고 생각해보자.

그 자료구조 즉 데이터베이스 테이블에 ‘15’라는 숫자가 들어있는지 확인하려면 어떻게 해야하는가?

만약 오름차순으로 정렬이 되어있지 않다면, 그냥 생으로 처음부터 한칸씩 열어보며 15가 있는지 없는지 확인을 할 수밖에 없다. 데이터의 숫자가 n일 때, O(n)이라는 성능이 나오게 된다.

만약 정렬이 되어있다면 조금 나을 것이다. 왜냐면 binary search라는 알고리즘을 사용해서 반씩 나누어서 찾다보면, O(log n)이라는 시간안에 해당 숫자를 (만약 있다면) 찾을 수 있기 때문이다.

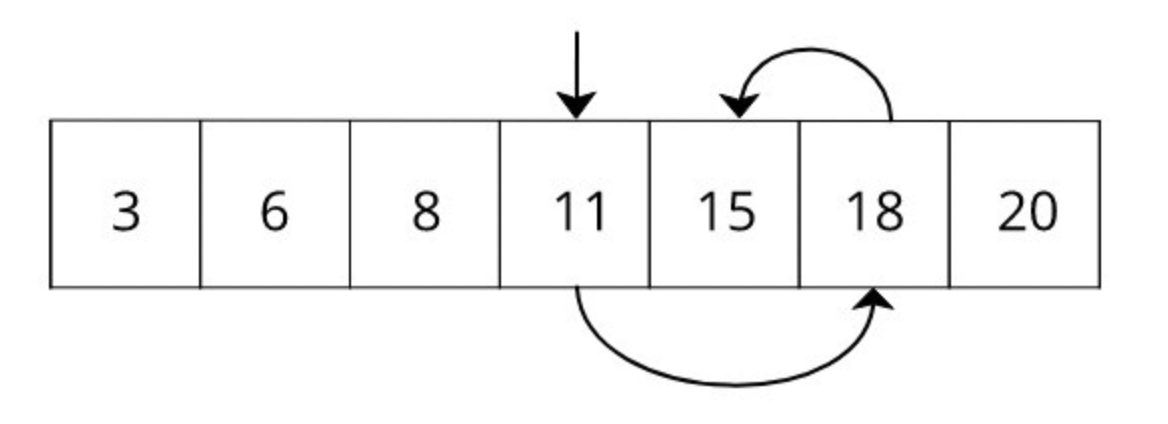
즉, binary search를 이용하면 원래 5번 걸려서 찾을 것이 3번이면 된다.

B-tree의 가장 단순한 종류인 binary tree도 이런 원리를 사용해 트리화 한 것인데, 차이는 물리적으로 리스트 안에 자료를 저장하기 보다는 reference 포인터를 이용해서 자료가 있는 디스크의 주소를 가르킨다는 점이다.

이런 점은 자료를 쓰는 write 작업의 효율성을 높여주게 되는데, 정렬된 리스트 같은 경우 숫자를 중간에 집어넣는 write 작업이 O(n)인 반면 (옆에 숫자들을 다 옴겨서 자리를 만들어줘야 하므로), binary tree의 경우는 그냥 맞는 자리를 찾은다음 슥 넣어주기만 하면 되므로 대체적으로 O(log n)의 성능을 가지게 된다.

그리고 이런 binary tree를 좀더 여러개의 자료를 담을 수 있는 형태로 쪼개서 발전 시킨 것이 b-tree라고 보면 되겠다. (binary tree는 노드에 숫자 한개, 따라서 각 노드의 자식 노드의 개수도 두개뿐이지만 b-tree는 각 노드당 담을 수 있는 숫자도 여러개고 한 노드의 자식 노드도 여러개다).

정리하자면 성능 차이는 아래와 같다.

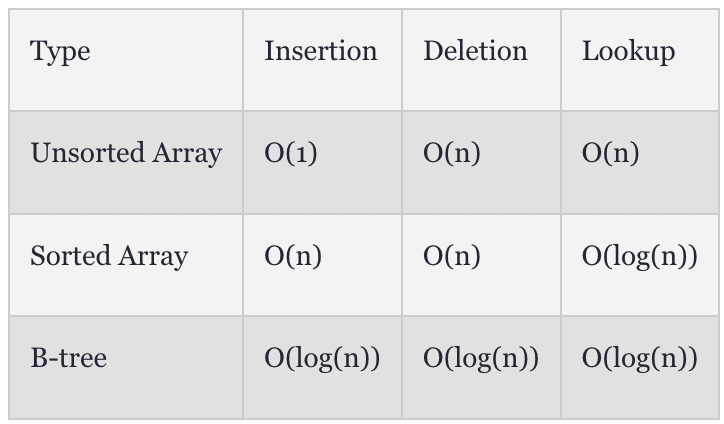
자료의 읽고 쓰는 작업의 속도가 가장 중요한 데이터베이스가 b-tree 자료구조를 쓰는 이유이다.

(B-tree는 binary tree와 달리 두갈래가 아닌 여러갈래로 쪼개지므로 엄밀한 성능은 예를 들어 log4 n 이 되므로 binary tree보다도 성능이 좋을 것이다).

B+tree란?

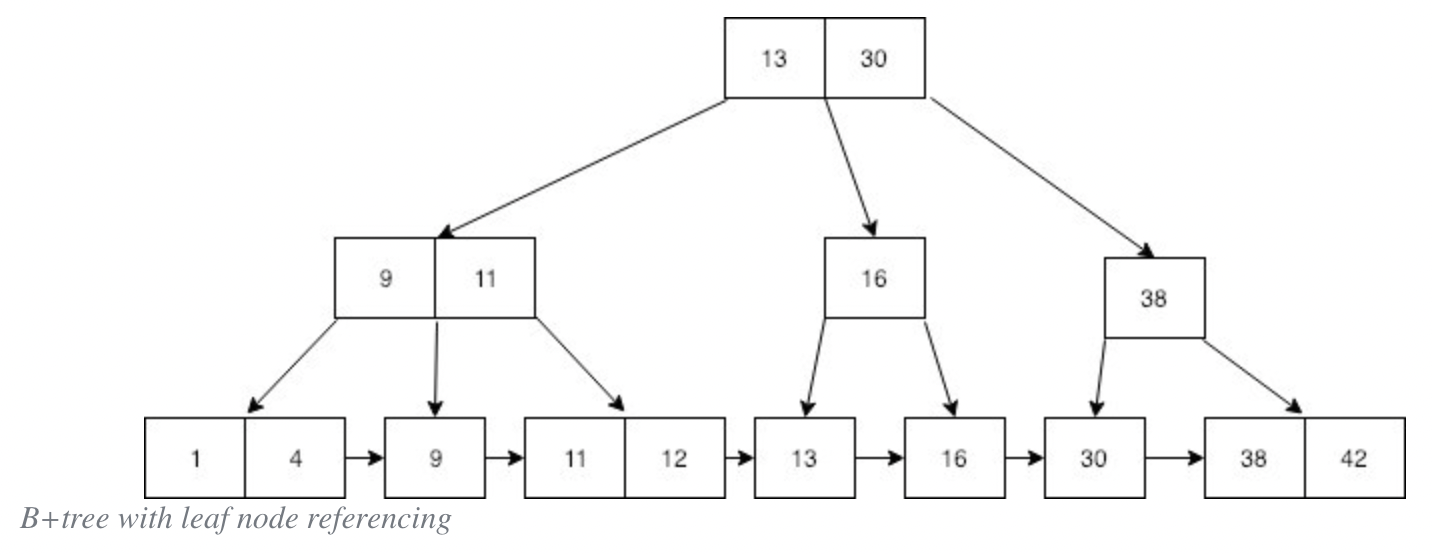
B+tree는 B-tree와 비슷한 자료구조로 B-tree와 상당히 비슷하게 생겼다. 차이점은 바로 모든 자료 즉 모든 숫자키가 가장 마지막 줄인 leaf 노드에 중복으로 들어간다는 점이다.

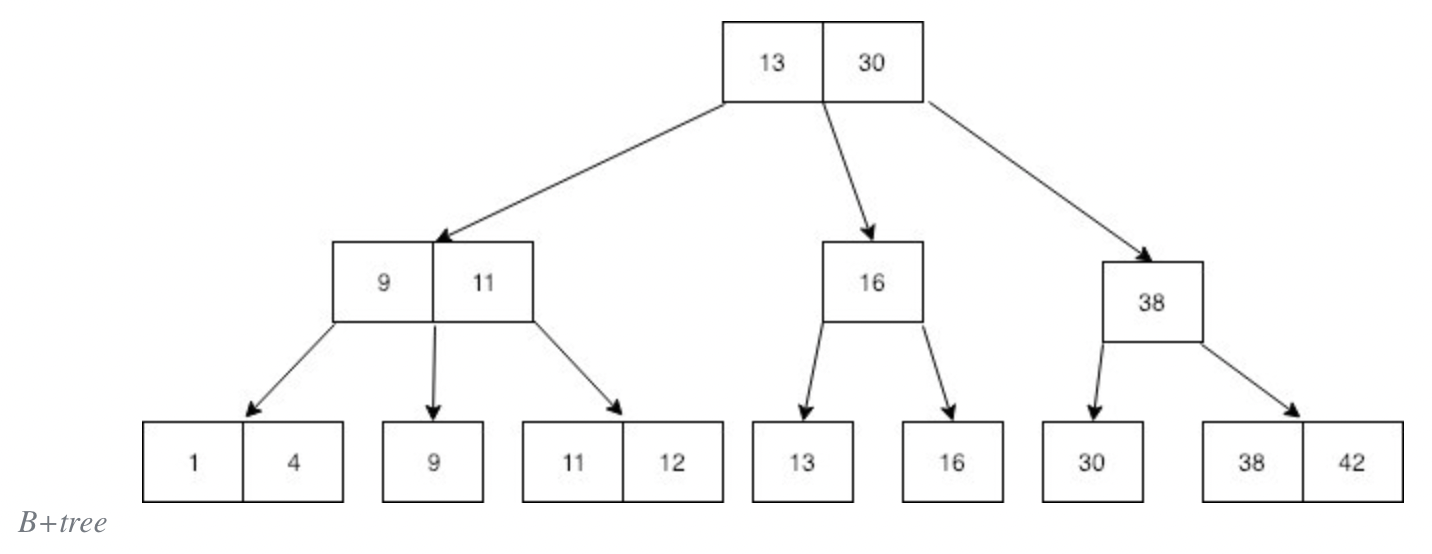
또한 모든 Leaf 노드는 오름차순으로 정렬되어 있는 것을 볼 수 있다. B+tree에서 leaf 노드들은 실제 ‘데이터가 저장되어지는 곳’으로 보면 되겠다.

추가적으로 만약 leaf 노드들 사이에도 추가 포인터들을 설치해준다면 순차적으로 모든 데이터를 순회하는 것 또한 가능하게 된다.

데이터베이스에 적용하기

위에 서술한 B-tree와 B+tree가 데이터베이스 인덱싱에 실제로 어떻게 사용되어지는지 보자.

이런 테이블이 있다고 해보자.

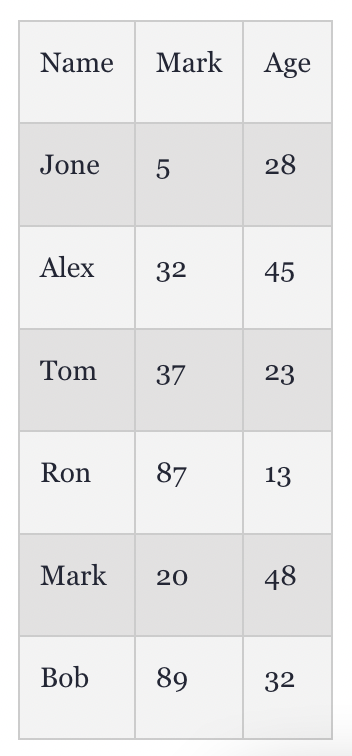
이름, 성적, 나이라는 세가지 컬럼이 있다.

이 데이터는 b+tree에 이렇게 저장된다.

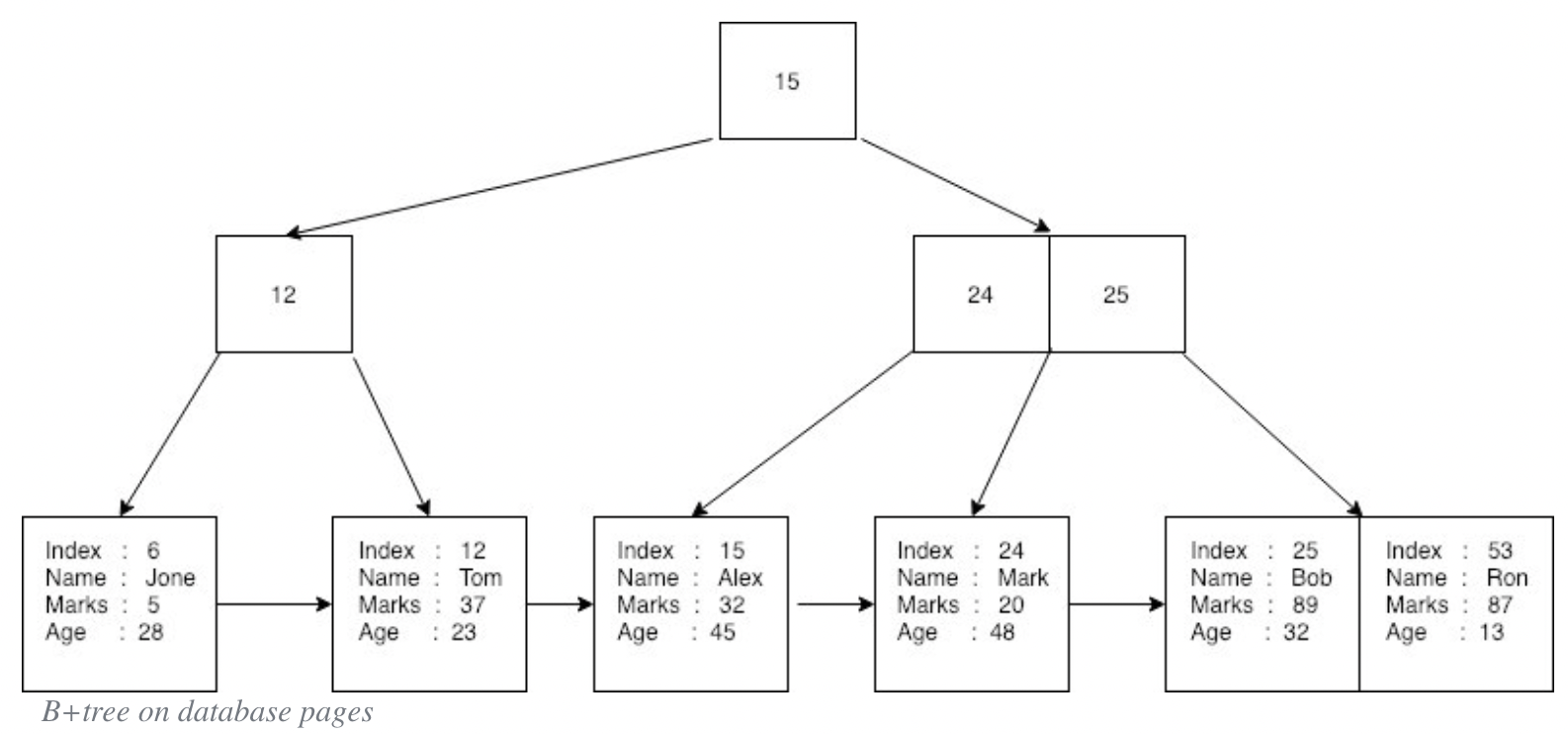
각 노드의 숫자는 각 데이터행의 primary key 가 되고, 맨 아래 leaf 노드들에 실제 데이터가 저장이 된다. 프라이머리 키로 데이터를 조회하고자 할 때 이런식의 데이터구조로 인해 빠른 조회가 가능하게 된다. 또한 각 데이터들도 오름차순으로 정렬이 되어있고 포인터가 존재하기 때문에, ‘key < 15’ 와 같은 범위적인 쿼리도 빨리 할 수 있고, 이름이 ‘Alex’ 인 사람을 찾는 것도 데이터를 순회하며 할 수 있다.

(테이블을 생성하면 기본적으로 primary key를기준으로 clustered index가 생성되는 것으로 알고 있는데, 이런 구조가 아닐까 싶다. 더 조사가 필요하다.)

만약 프라이머리 키가 아닌 다른 값, 예를 들어 이름으로 조회 쿼리를 많이 한다고 한다면 ‘Name’ 컬럼에 인덱스를 매겨주는 것이 좋은 방법일 것이다. 이런 추가적 인덱스, 즉 non-clustered index는 b-tree에 생성이 된다.

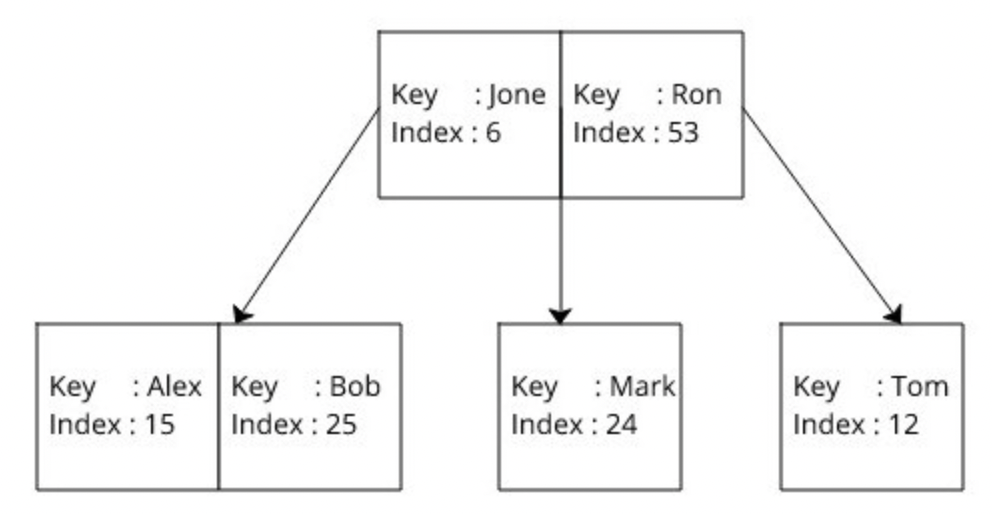
각 노드는 key, value를 가지게 되는데 이 때 key는 인덱스 컬럼의 값 (이름) 그리고 value는 실제 데이터가 저장된 곳을 찾을 수 있는 값, 즉 프라이머리 키의 값이다. b-tree는 key를 기준으로 정렬이 된다.

만약 ‘Alex’라는 사람을 찾고자 한다면 이 B-tree에서 해당 노드를 찾아서 프라이머리 키 값을 조회한 후, 자료가 저장되어 있는 B+tree에서 해당 프라이머리 키 값을 사용해 나머지 데이터를 조회하면 되는 것이다. O(log n) 조회를 두번 해야 하기 때문에 바로 clustered index를 이용해 조회하는 것보단 약간 느릴 것을 예상할 수 있다.

이상으로 데이터베이스에서 쓰이는 자료구조인 B-tree와 B+tree에 대해서 알아보았다.

Reference: https://dzone.com/articles/database-btree-indexing-in-sqlite